Iteration techniques for Non-linear analysis

Iteration techniques for Non Linear analysis.

Static structural analysis, in one way, can be classified into linear and non linear analysis. When response of the structure like displacement, stress and strain, varies linearly in proportional to the magnitude of applied load, then it can be categorized as linear static analysis. And when the structure responses does not vary in proportion to the magnitude of applied load, then it can be called as non linear analysis.

Whatever be the type of analysis, the solver deals with solving the basic equation of Force = stiffness matrix * deformation. Here the stiffness matrix consists of material properties like rigidity modulus, elastic modulus etc and geometric parameters like cross section area, length, moment of inertia etc. Static analysis assumes that these above mentioned  parameters do not change at the time when structure is loaded. And on the other hand, non linear static analysis considers the changes in these parameters when load is applied to the structure. These changes are accounted in to the analysis by recalculating the stiffness matrix using deformed structure and updated property after each steps of load application. 

Types of Non Linearities

1) Geometric non linearity - When the geometric condition ie. the geometric cross section of loaded structure changes due to large deformation, then the geometric non linearity comes into play. The deformations and rotations are at minute levels in linear static analysis, whereas both the deformations and rotations are at larger magnitudes for non linear static analysis. 

2) Material non linearity - Basically all the engineering materials are non linear in nature either after a certain point of loading or even at the starting of loading. Generally the metals exhibit non linear stress strain behavior after their elastic limit that is when they enter plastic zone. Non metals exhibit non linear stress strain curve even from the origin itself. Material non linearity can be classified in detail as 

a) Linear elastic - perfectly plastic 

b) Linear elastic - plastic

c) Non linear elastic

d) Hyper elastic 

3) Contact/Boundary non linearity - When surfaces of two or more bodies come into or out of contact during the course of analysis study, then there arises the contact non linearity. The gap between the bodies can be modelled with a spring of specified value of stiffness. Greater the stiffness coefficient, lesser the penetration of one surface to another, whereas lesser the stiffness coefficient, more the penetration. In contact non linearity, K is a function of nodal displacement. So as during the stage of deformation, stiffness matrix K constantly needs to get updated as a result of displacement of nodes. Contact non linearity arises when deformation of one part brings deformation or change in geometry  on the other part in contact, and thus changes the stiffness matrix during solving process.

Common iteration techniques for non linear problems.

Both the geometric and material non linearities are best solved using Newton Raphson method and Modified Newton Raphson method.  And penalty method is used for solving contact non linearity problems. 

As of now, let us dive into Newton Raphson method.

 

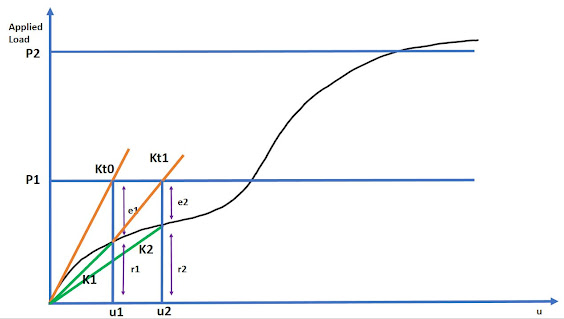
Here is Newton Raphson method applied to force displacement curve. The force displacement is actually not known to the user. Let the goal is to find the displacement at load P. Here the load P is divided into two increments for simplification as P1 and P2. Let j represents the number of increments and i represents the number of iterations within the jth increment.

 

Let u be the displacement, P be load applied, P1 and P2 be the incremental loads, r be the reaction offered by the structure, e be the error ( difference between the applied load P and structure reaction), Kt0 be the tangent stiffness and K be the secant stiffness of material.

We assume some initial conditions for the start of iteration. 

initial displacement u0 = u final|Pj-1 = 0

initial reaction r0 = r final|Pj-1 = 0

load error e0 = Pj - r0 = P1

Tangent stiffness Kt0 is calculated by using the formula of 

Kt0 = K0 + (dK/du)x u0, 

where as displacement estimation is carried out by the formula of

 u1 = u0 + (Pj-r0)/Kt0 

Here for the first iteration, K0 is found out from the elastic stiffness value. It can be clearly justified in such a way that every non linear behavior of material starts after the elastic response of the material  ceases. So the initial K0 for the first iteration process can be taken from the stiffness value of elastic stage. So the u1 is found out when Kt0 tangent stiffness meets the P1 increment. The displacement value corresponding to the meeting point is noted as u1. 

A brief understanding on types of stiffness. The stiffness matrix on F = K*x equation is a combination of material and geometrical stiffness. In non linear cases, for a softening material, material stiffness K = tangent stiffness (Kt) -  geometric stiffness (K). Where as for a hardening material, material stiffness K = tangent stiffness (Kt) + geometrical stiffness (K).The geometrical stiffness does not depend on material properties and is purely depend on the load applied and the geometric state of element ( say structure) during the course of application of load. For a linear analysis, the structure deformation is considered very small. As a result of which, the contribution of geometric stiffness is negligible. So the tangent stiffness Kt is same as material stiffness.

Back to solver iteration, The secant stiffness ( here secant stiffness = Kt - geometric stiffness) is found out using the displacement u1 and is extended from origin to meet vertical line at u1 displacement. This is the point along which the actual Force vs displacement curve pass through ( which is unknown to the user as of now).

 

The structure reaction force r1 is found out by multiplying the Secant stiffness K1 with u1. 

r1 = K1 x u1

Actually the applied incremental load P1 and the reaction force developed need to be same at the exact displacement stage. Greater the magnitude of error, more the number of iterations needed to be carried out to make the structure reaction force  converge to the applied load value. The displacement at which the reaction force developed matches with the applied load, then  that displacement is the exact response of the system to the externally applied load.

where, error e1 = Pj - r1

 

Iteration 2 ( i = 2)

As the error found out during the first iteration falls out of the specified range of convergence, the solver proceeds to the iteration 2 ( i=2) within the same increment ( j=1). The tangent stiffness Kt1 is found out

Kt1 = K1 + (dK/du) x u1

And displacement u2 being estimated with,

u2 = u1 + (P1-r1)/Kt1.

As similar process to iteration1, the secant stiffness ie, the geometric stiffness corresponding to the displacement u2 is found out to obtain the second point of force displacement curve.

 

 

The structure response r2 is found out using

r2 = K2 * u2 

And the load error e2 is found out by 

e2 = P1 - r2

 

Even then the structure reaction and externally applied load P1 do not converge, there arises the need to undergo third iteration i =3 within the same increment j=1.

Iteration 3:

 

 

On following the same procedures of iteration 1 and iteration 2, the error comes out to be negligible. That is, the reaction force at displacement u3 came out to be equal to the load increment P1. And this marks the end of first incremental load P1.

Increment j = 2:

The stiffness "K", structure reaction response "r" and displacement "u" of the final iteration of previous increment is used as input parameters for the initial iteration of next increment. 

 

The steps followed in first load increment P1 is repeated in the next load increment P2 to finally reach the destination of displacement at load P2. Once the displacement is found, the other structure responses like strain, stress etc can be estimated.

Modified Newton Raphson method.

Modified Newton Raphson method is similar to Newton Raphson method, where as like previous  case, solver start with finding  tangent stiffness Kt0 and thus the corresponding displacement u1. Then the error and reaction force are found out using the same equations of Newton Raphson method. As when the error do not falls within the range, solver proceeds to next iteration within the same increment. But here in Modified Newton Raphson method, solver do not update the tangent stiffness on upcoming iterations as it proceed with the same Kt0 throughout the process till the solution converge. Thus Modified Newton Raphson method is computationally effective method of solving the problem as calculation of stiffness matrix for all the iterations is tedious task. The number of iterations is more in this case which is far less computationally expensive than recalculating the stiffness matrixes.